Install numpy
pip install numpy
Import numpy in code
import numpy as np
What a ndarray is?
It is a central data structure of the NumPy library.
It represents a homogeneous n-dimensional array object.
it has methods to describe it and efficiently operate on it.
ndarray properties
– ndarray is not a Python list(conceptually and in terms of object hierarchy).
Among other things:
* contrary to lists, all elements in a ndarray should be homogeneous.
* ndarray are immutables: to add or delete elements we need to recreate a new ndarray but to
update existing elements we don’t need.
* methods and properties are very different.
– axes, shape and size:
In NumPy, dimensions are called axes(ndim int property).
The shape specifies the sizes of each dimension(shape tuple property ).
The size represents the total number of elements of the array(size int property).
This means that if you have a 2D array that looks like this:
[ [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12] ] |
We can also represent it in that way graphically:
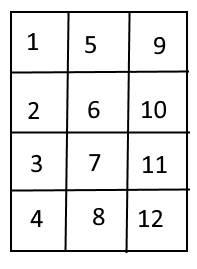
Axes :
2
The shape is defined for axes as :
– The first axis has a length of 3
– The second axis has a length of 4.
Size : 12
create ndarray with 1 dimension:
ndarray_1_dimension: np.ndarray = np.array((1, 5, 10), dtype=int) print(f'ndarray_1_dimension={ndarray_1_dimension}')#ndarray_with_a_single_dimension=[ 1 5 10] # equivalence ndarray_1_dimension: np.ndarray = np.array([1, 5, 10], dtype=int) print(f'ndarray_1_dimension={ndarray_1_dimension}')#ndarray_with_a_single_dimension=[ 1 5 10] |
create a ndarray with 2 dimensions and retrieve basic information of it
a: np.ndarray = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) print(f'a={a}') print(f'a.ndim={a.ndim}') print(f'a.size={a.size}') # a tuple of integers that indicate the number of elements stored # along each dimension of the array. print(f'a.shape={a.shape}') |
output:
a=[[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] a.ndim=2 a.size=12 a.shape=(3, 4) |
tuple of numpy int created from a ndarray with a single dimension
tuple_of_numpy_int: tuple[np.ndarray] = tuple(np.array((1, 5, 10), dtype=int)) print(f'tuple_of_numpy_int={tuple_of_numpy_int}')#tuple_of_numpy_int=(1, 5, 10) |
Iterate over a ndarray
Iterate two dimension array by row
a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] for row in a: print(f'row={row}') # row=[1 2 3] # row=[4 5 6] # row=[7 8 9] |
access and modify elements by index of a 2 dimensions ndarray
Important: modifying existing elements of a ndarray doesn’t require to recreate a new object.
basic indexing
access to a single value and modify it
-----ACCESS TO A SINGLE VALUE a=[[1 2 3] [4 5 6] [7 8 9]] a[0,2]=3 a[2,1]=8 print(f'-----MODIFY A SINGLE VALUE') a[0, 2] = 99 print(f'a={a}') # a=[[ 1 2 99] # [ 4 5 6] # [ 7 8 9]] |
access to a single row and modify it
print(f'-----ACCESS TO A ROW') a = np.arange(1, 10).reshape((3, 3)) print(f'a={a}') # a=[[1 2 3] # [4 5 6] # [7 8 9]] print(f'a[0]={a[0]}') # a[0]=[1 2 3] print(f'-----MODIFY A ROW') a[0] = [1, 8, 5] print(f'a={a}') # a=[[1 8 5] # [4 5 6] # [7 8 9]] |
access to multiple elements via array indexing
We index the array by providing an array of rows and an array of columns.
These 2 arrays (rows and cols) have to have the same size.
print(f'-----ACCESS TO TWO ELEMENTS') a = np.arange(1, 10).reshape((3, 3)) print(f'a={a}') # a=[[1 2 3] # [4 5 6] # [7 8 9]] rows = [1, 2] # We specify 2 row indexes cols = [0, 1] # same thing for columns print(f'a[rows, cols] ={a[rows, cols]}') # a[rows, cols] =[4 8] print(f'-----MODIFY THE VALUE OF THESE ELEMENTS') a[rows, cols] = 0 print(f'a after modification=\n{a}') # a after modification= # [[1 2 3] # [0 5 6] # [7 0 9]] print(f'-----ACCESS TO THREE ELEMENTS') a = np.arange(1, 10).reshape((3, 3)) print(f'a={a}') # a=[[1 2 3] # [4 5 6] # [7 8 9]] rows = [0, 1, 2] # We specify 3 row indexes cols = [2, 2, 1] # same thing for columns print(f'a[rows, cols] ={a[rows, cols]}') # a[rows, cols] =[3 6 8] print(f'-----MODIFY THE VALUE OF THESE ELEMENTS') a[rows, cols] = 0 print(f'a after modification=\n{a}') # a after modification= # [[1 2 0] # [4 5 0] # [7 0 9]] |
Insert and delete elements in a ndarray
Important: inserting and deleting elements means changing the size of the ndarray object,
so any of these operations return a new object.
Here are the signatures of the methods we want to use:
def delete(arr: Union[ndarray, Iterable, int, float], obj: Union[slice, int, ndarray,
Iterable, float[int]], axis: Optional[int] = None) -> ndarray
def append(arr: Union[ndarray, Iterable, int, float], values: Union[ndarray, Iterable,
int, float], axis: Optional[int] = None) -> ndarray
def insert(arr: Union[ndarray, Iterable, int, float], obj: Union[int, slice,
Iterable[int]], values: Union[ndarray, Iterable, int, float], axis: Optional[int] = None) ->
ndarray
We can notice that these methods are very close but don’t have exactly the same parameters.
We will not detail each difference, but we have to remember that we cannot interchange call
of
the method and keeping the same nature of parameters because these may have a different
meaning.
There is multiple ways to select the elements we want to insert and delete, we will show the
selection:
– By index
– By the where() function
Insert and delete elements in a 1d ndarray
Examples covering most of cases:
import numpy as np print(f'-----DELETE ELEMENTS IN ONE DIMENSION NDARRAY') print(f'-----DELETE ELEMENTS BY INDEX ') a: np.ndarray = np.arange(start=1, step=1, stop=10) print(f'a_ndarray={a}') # a_ndarray=[1 2 3 4 5 6 7 8 9] result: np.ndarray = np.delete(a, [1, 3]) print(f'result={result}') # result=[1 3 5 6 7 8 9] print(f'-----DELETE ELEMENTS AT THE INDEXES COMPUTED BY THE WHERE FUNCTION ') a: np.ndarray = np.arange(start=10, step=1, stop=20) print(f'a={a}') # a=[10 11 12 13 14 15 16 17 18 19] result: np.ndarray = np.delete(a, np.where(a > 12)) print(f'result={result}') # result=[10 11 12] print(f'-----INSERT ELEMENT(S) AT THE END') a: np.ndarray = np.arange(start=10, step=1, stop=20) print(f'a={a}') # a=[10 11 12 13 14 15 16 17 18 19] result: np.ndarray = np.append(a, [21, 22]) print(f'result={result}') # result=[10 11 12 13 14 15 16 17 18 19 21 22] print(f'-----INSERT ELEMENT(S) ANYWHERE') a: np.ndarray = np.arange(start=10, step=1, stop=20) print(f'a={a}') # a=[10 11 12 13 14 15 16 17 18 19] result: np.ndarray = np.insert(a, 0, [9, 1, 9]) print(f'result={result}') # result=[ 9 1 9 9 10 11 12 13 14 15 16 17 18 19] print(f'-----INSERT ELEMENT(S) ANYWHERE WITH THE WHERE FUNCTION') a: np.ndarray = np.arange(start=10, step=1, stop=20) print(f'a={a}') # a=[10 11 12 13 14 15 16 17 18 19] where: np.ndarray = np.where(a == 12) print(f'where={where}, type={type(where)}') # where=(array([2], dtype=int64),), type=<class 'tuple'> result: np.ndarray = np.insert(a, np.where(a == 12)[0], [1, 2, 3]) print(f'result={result}') # result=[10 11 1 2 3 12 13 14 15 16 17 18 19] |
Insert and delete elements in a 2d ndarray
With 2-dimensions ndarray, a very important point is the optional axis parameter
that we didn’t need to specify with 1-dimension ndarray.
delete() and insert() functions use this parameter in the exact same
way:
axis – axis along which to delete the subarray defined by `obj`.
If `axis` is None, `obj` is applied to the flattened array.
axis – axis along which to insert `values`.
If `axis` is None then `arr` is flattened first.
What we want to remember:
– The default value is None: the ndarray will be flattened.
– 0 : the operation will be executed in the row axis(Concretely for
insert(),delete(), elements will respectively be added as rows and
deleted by rows)
– 1 : the operation will be executed in the column axis(Concretely for insert(),delete(),
elements will respectively be added as columns and deleted by column)
Examples covering most of cases:
import numpy as np print(f'-----DELETE ELEMENTS IN 2-DIMENSION NDARRAY') print(f'-----DELETE SPECIFIC AND FLATTENED ELEMENTS BY INDEX WITH DEFAULT AXIS(NONE) ') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.delete(a, [1, 3]) print(f'result=\n{result}') # result=[1 3 5 6 7 8 9] print(f'-----DELETE ROWS AT THE INDEXES COMPUTED BY THE WHERE FUNCTION ') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] print(f'We delete rows where the second element is less than 4') np_where = np.where(a[:, 1] < 4) print(f'np_where={np_where}') result: np.ndarray = np.delete(a, np.where(a[:, 1] < 4), axis=0) print(f'result=\n{result}') # result= # [[4 5 6] # [7 8 9]] print(f'We delete rows according to a where condition pertaining both rows and columns') a: np.ndarray = np.array([[101, 383], [101, 513], [191, 632]]) # transpose= # [[101 383] # [101 513] # [191 632]] n = np.where((a[:, 1] == 513) & (a[:, 0] == 101)) print(f'n={n}') merge_locations_with_best_match_first = np.delete(a, np.where((a[:, 1] == 513) & (a[:, 0] == 101)), 0) print(f'merge_locations_with_best_match_first=\n{merge_locations_with_best_match_first}') # merge_locations_with_best_match_first= # [[101 383] # [191 632]] print(f'-----DELETE COLUMNS AT THE INDEXES COMPUTED BY THE WHERE FUNCTION') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] print(f'We delete columns where the third element is more than 7') np_where = np.where(a[2, :] > 7) print(f'np_where={np_where}') result: np.ndarray = np.delete(a, np.where(a[2, :] > 7), axis=1) print(f'result=\n{result}') # result= # [[1] # [4] # [7]] print(f'-----DELETE ALL ELEMENTS BY INDEX WITH ROW AXIS (0) ') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.delete(a, [1, 2], axis=0) print(f'result={result}') # result=[[1 2 3]] print(f'-----DELETE ALL ELEMENTS BY INDEX WITH COLUMN AXIS (1) ') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.delete(a, [1, 2], axis=1) print(f'result=\n{result}') # result= # [[1] # [4] # [7]] print(f'-----INSERT ELEMENT(S) AT THE END') print(f'* INSERT 1 ROW AT THE END') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.append(a, [[21, 22, 23]], axis=0) print(f'result=\n{result}') # result=[ # [ 1 2 3] # [ 4 5 6] # [ 7 8 9] # [21 22 23]] print(f'* INSERT 2 ROWS AT THE END') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.append(a, [[21, 22, 23], [31, 32, 33]], axis=0) print(f'result=\n{result}') # result=[ # [[ 1 2 3] # [ 4 5 6] # [ 7 8 9] # [21 22 23] # [31 32 33]] print(f'-----INSERT ELEMENT(S) ANYWHERE') print(f'* INSERT ROWS AT THE BEGINNING') a = np.arange(1, 10).reshape((3, 3)) print(f'a_ndarray=\n{a}') # a_ndarray= # [[1 2 3] # [4 5 6] # [7 8 9]] result: np.ndarray = np.insert(a, 0, [[21, 22, 23], [31, 32, 33]], axis=0) # result: np.ndarray = np.insert(a, 0, [9, 1, 9]) print(f'result=\n{result}') # result= # [[21 22 23] # [31 32 33] # [ 1 2 3] # [ 4 5 6] # [ 7 8 9]] # print(f'-----INSERT ELEMENT(S) ANYWHERE WITH THE WHERE FUNCTION') # a: np.ndarray = np.arange(start=10, step=1, stop=20) # print(f'a={a}') # # a=[10 11 12 13 14 15 16 17 18 19] # where: np.ndarray = np.where(a == 12) # print(f'where={where}, type={type(where)}') # # where=(array([2], dtype=int64),), type=<class 'tuple'> # result: np.ndarray = np.insert(a, np.where(a == 12)[0], [1, 2, 3]) # print(f'result={result}') # # result=[10 11 1 2 3 12 13 14 15 16 17 18 19] |
Search elements depending on condition: the where() function.
Here is it’s signature:
def where(condition: Union[ndarray, Iterable, int, float, bool], x: Union[ndarray, Iterable, int, float] = None, y: Union[ndarray, Iterable, int, float] = None) -> ndarray |
it returns an array with elements from `x` where `condition` is True, and elements from `y`
elsewhere.
beware: providing only condition parameter is a corner case of the where()
function,this is equivalent to np.asarray(condition).nonzero(), so it returns
indexes of matches and not the value of the matches.
Examples with one condition and no x,y parameters provided: returns indexes of matches
a: np.ndarray = np.arange(start=1, step=2, stop=20) print(f'a_ndarray={a}') # a_ndarray=[ 1 3 5 7 9 11 13 15 17 19] result: ndarray = np.where(a > 5) print(f'result={result}') # result=(array([3, 4, 5, 6, 7, 8, 9], dtype=int64),) print(f'* THE LAST ONE IS EQUIVALENT TO') result: ndarray = np.asarray(a > 5).nonzero() print(f'result={result}') # result=(array([3, 4, 5, 6, 7, 8, 9], dtype=int64),) print(f'* WITH AND CONDITION') result: ndarray = np.where((a > 5) & (a < 8)) print(f'result={result}') # result=(array([3], dtype=int64),) print(f'* WITH OR CONDITION') result: ndarray = np.where((a > 5) | (a < 8)) print(f'result={result}') # result=(array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype=int64),) |
Examples with one condition and x,y parameters provided: returns values of match
# It is the general case of the where() function: the matches return the values<br/>print(f'a_ndarray={a}') # a_ndarray=[ 1 3 5 7 9 11 13 15 17 19] result: ndarray = np.where(a > 5, a, -1) print(f'result={result}') # result=[-1 -1 -1 7 9 11 13 15 17 19] print(f'* WITH AND CONDITION') result: ndarray = np.where((a > 5) & (a < 10), a, -1) print(f'result={result}') # result=[-1 -1 -1 7 9 -1 -1 -1 -1 -1] print(f'* WITH OR CONDITION') result: ndarray = np.where((a > 5) | (a < 3), a, -1) print(f'result={result}') # result=[ 1 -1 -1 7 9 11 13 15 17 19] |
use case: filter close points of 2 1d-ndarray objects representing respectively rows and columns
– At the beginning we create a dummy ndarray of boolean with only 4 points set to
the true
value.
These 4 points represent the points we want to process.
– Indeed we accept only true values(nonzero()).
The result of the first filtering is stored in the variable loc.
That is a tuple of two ndarrays: the first one represents the row indexes and the second
one represents the column indexes.
So elements of the same index of the 2 arrays represent coordinates.
– At last we remove elements which distances are close, that is less than 50 both in horizontal
and in vertical.
Note: since ndarrays are immutables we need to recreate a new ndarray to
make changes persistent.
from typing import List import numpy as np print('#### WE CREATE A DUMMY NDARRAY WITH ONLY 4 POINTS SET TO TRUE####') # 101,490 - 101,513 - 191,631 - 191,632 res_threshold: np.ndarray = np.zeros((600, 800), dtype=bool) rows = (101, 101, 191, 191) columns = (490, 513, 631, 632) columns_ = res_threshold[rows, columns] res_threshold[rows, columns] = True print(f'res_threshold={res_threshold}, type={type(res_threshold)}') print('#### KEEP MATCHING POINTS ') loc: tuple[np.ndarray, np.ndarray] = res_threshold.nonzero() print(f'loc={loc}') print('####REMOVING MATCHING POINTS VERY CLOSE') elements_index_to_remove: List[int] = [] for i, pt in enumerate(zip(loc[1][:-1], loc[0][:-1])): if abs(loc[1][i + 1] - loc[1][i]) < 50 and abs(loc[0][i + 1] - loc[0][i]) < 50: elements_index_to_remove.append(i) print(f'elements_index_to_remove={elements_index_to_remove}') print('####RECREATE A NEW NDARRAY') x: np.ndarray = np.delete(loc[0], elements_index_to_remove) y: np.ndarray = np.delete(loc[1], elements_index_to_remove) merged_loc = (x, y) print(f'merged_loc={merged_loc}') |
Output:
#### WE CREATE A DUMMY NDARRAY WITH ONLY 4 POINTS SET TO TRUE#### res_threshold=[[False False False ... False False False] [False False False ... False False False] [False False False ... False False False] ... [False False False ... False False False] [False False False ... False False False] [False False False ... False False False]], type=<class 'numpy.ndarray'> #### KEEP MATCHING POINTS loc=(array([101, 101, 191, 191], dtype=int64), array([490, 513, 631, 632], dtype=int64)) ####REMOVING MATCHING POINTS VERY CLOSE elements_index_to_remove=[0, 2] ####RECREATE A NEW NDARRAY merged_loc=(array([101, 191], dtype=int64), array([513, 632], dtype=int64)) |
Variant use case: Same thing by preserving a specific point(That is a couple of column-row) in case of close points
It is needed when we want to keep the best matching with the exact coordinates while filtering
out closer points.
Here is how we process:
– At the beginning we create a dummy ndarray of int
with only 4 points set to a value superior to 0.
These 4 points represent the points we want to process.
– As previously, The result of the first filtering is stored in the variable
loc.
– But here we have an additional step, indeed we compute the index of the max value (variable
max_value_ndarray_index) because when
we will merge close points in the next step, we always want to keep the best point.
– Indeed we can see at the end of the program that the max value is kept in the final result,
contrary to the previous use case where we didn’t be careful to keep it in case of comparison.
from typing import List import numpy as np print(f'-----WE CREATE FAKE MATCHING COORDINATES') rows = (101, 101, 191, 191) columns = (490, 513, 631, 632) # 101-490 will have the max value res_before_threshold: np.ndarray = np.zeros((600, 800)) res_before_threshold[rows, columns] = 0.8 res_before_threshold[101, 490] = 0.85 print(f'res_before_threshold={res_before_threshold}') print(f'#####RETRIEVE THE COORDINATE OF THE MAX VALUE') max_value_flatten_index = np.argmax(res_before_threshold) print(f'max_value_flatten_index={max_value_flatten_index}') max_value_ndarray_index: tuple[np.ndarray] = np.unravel_index(max_value_flatten_index, res_before_threshold.shape) print(f'max_value_ndarray_index={max_value_ndarray_index}, type={type(max_value_ndarray_index)}') print('#### KEEP MATCHING POINTS ') print('#### WE EXPECT TO HAVE THE 4 VALUES WE SET PREVIOUSLY####') # 101,490 - 101,513 - 191,631 - 191,632 loc: tuple[np.ndarray, np.ndarray] = res_before_threshold.nonzero() print(f'loc={loc}, type={type(loc)}') print('####REMOVING MATCHING POINTS VERY CLOSE') elements_index_to_remove: List[int] = [] for i, pt in enumerate(zip(loc[1][:-1], loc[0][:-1])): if abs(loc[1][i + 1] - loc[1][i]) < 50 and abs(loc[0][i + 1] - loc[0][i]) < 50: if loc[1][i] == max_value_ndarray_index[1] and loc[0][i] == max_value_ndarray_index[0]: elements_index_to_remove.append(i + 1) else: elements_index_to_remove.append(i) print(f'elements_index_to_remove={elements_index_to_remove}') print('####RECREATE A NEW NDARRAY') x: np.ndarray = np.delete(loc[0], elements_index_to_remove) y: np.ndarray = np.delete(loc[1], elements_index_to_remove) merged_loc = (x, y) print(f'merged_loc={merged_loc}') |
Output:
-----WE CREATE FAKE MATCHING COORDINATES res_before_threshold=[[0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] ... [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.]] #####RETRIEVE THE COORDINATE OF THE MAX VALUE max_value_flatten_index=81290 max_value_ndarray_index=(101, 490), type=<class 'tuple'> #### KEEP MATCHING POINTS #### WE EXPECT TO HAVE THE 4 VALUES WE SET PREVIOUSLY#### loc=(array([101, 101, 191, 191], dtype=int64), array([490, 513, 631, 632], dtype=int64)), type=<class 'tuple'> ####REMOVING MATCHING POINTS VERY CLOSE elements_index_to_remove=[1, 2] ####RECREATE A NEW NDARRAY merged_loc=(array([101, 191], dtype=int64), array([490, 632], dtype=int64)) |
use case: convert 2 1d-ndarray objects representing respectively rows and columns to a ndarray of 2 dimensions
It is required when we use functions that divide the result into 2 1d-ndarrays (a first one
representing the column indexes and a second one representing the row indexes) and that we want
to recreate a ndarray of 2 dimensions with them.
For example the instance method nonzero() does that.
To reverse the axes we use the function transpose().
For example with nonzero():
import numpy as np res: tuple[np.ndarray, np.ndarray] = foo_ndarray.nonzero() transpose: np.ndarray = np.transpose(res) |
Or with a simple executable example:
import numpy as np first_ndarray: np.ndarray = np.arange(start=1, step=1, stop=10) second_ndarray: np.ndarray = np.arange(start=2, step=2, stop=20) print(f'first_ndarray={first_ndarray}') print(f'second_ndarray={second_ndarray}') transpose: np.ndarray = np.transpose((first_ndarray, second_ndarray)) print(f'transpose={transpose}') |
Output:
first_ndarray= [ 1 2 3 4 5 6 7 8 9] second_ndarray=[ 2 4 6 8 10 12 14 16 18] transpose=[[ 1 2] [ 2 4] [ 3 6] [ 4 8] [ 5 10] [ 6 12] [ 7 14] [ 8 16] [ 9 18]] |
Use case: reverse rows or columns or both
import numpy as np a: np.ndarray = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) a_reversed_column_and_row = a[::-1, ::-1] print(f'a=\n{a}') print(f'a_reversed_column_and_row=\n{a_reversed_column_and_row}') print('-----------') a: np.ndarray = np.array([[1, 2], [3, 4], [5, 6]]) a_reversed_column = a[:, ::-1] print(f'a=\n{a}') print(f'a_reversed_column=\n{a_reversed_column}') print('-----------') a: np.ndarray = np.array([[1, 2], [3, 4], [5, 6]]) a_reversed_row = a[::-1, :] print(f'a=\n{a}') print(f'a_reversed_row=\n{a_reversed_row}') |
Output:
a= [[ 1 2 3 4] [ 5 6 7 8] [ 9 10 11 12]] a_reversed_column_and_row= [[12 11 10 9] [ 8 7 6 5] [ 4 3 2 1]] ----------- a= [[1 2] [3 4] [5 6]] a_reversed_column= [[2 1] [4 3] [6 5]] ----------- a= [[1 2] [3 4] [5 6]] a_reversed_row= [[5 6] [3 4] [1 2]] |
What a dtype is?
ndarray elements all known as dtype.
Concretely it doesn’t mean that elements objects are
derived from this type, it is a conceptual type.
unit testing with numpy
Assert two array_like objects are equal:
assert_array_equal(x, y[, err_msg, verbose])
